Suitable for most UR and AUBO 6-DOF robots

1.MDH coordinate system establishment

The robot coordinate system is constructed using MDH (improved DH) method to prepare for setting the user coordinate system in the virtual machine later. The DH coordinate system established according to the size diagram of the robot is shown in the figure, and the base coordinate system coincides with the world coordinate system when the robot bracket is fixed.

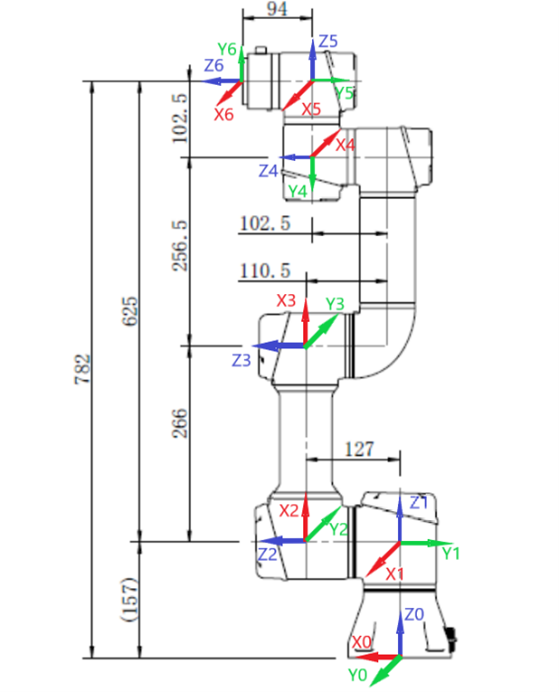
According to the X and Z axes and the size of the robot, four DH parameters α, a, theta, and d of the robot can be established, as shown in the table below.

In MATLAB, use the toolbox Robotics Toolbox to model, and the simulation interface is shown in the figure.

2.Forward kinematics analysis of robot

The MDH coordinate system is established and the transformation matrix of the neighbouring joints is shown in the following equation. Where cθi is cosθi and sθi is cosθi.

$$i^{i-1}\boldsymbol{T}=Rot(x{i-1},\alpha_i)Trans(x_{i-1},a_i)Rot(z_i,\theta_i)Trans(z_i,d_i)$$

$$i^{i-1}\boldsymbol{T}=\begin{bmatrix}c\theta_i&-s\theta_i&0&a{i-1}\s\theta_ic\alpha_{i-1}&c\theta_ic\alpha_{i-1}&-s\alpha_{i-1}&-s\alpha_{i-1}d_i\s\theta_is\alpha_{i-1}&c\theta_is\alpha_{i-1}&c\alpha_{i-1}&c\alpha_{i-1}d_i\0&0&0&1\end{bmatrix}$$

By substituting the above DH parameters into the above formula, the transformation matrix can be obtained:

$$_1^0\boldsymbol{T}=\begin{bmatrix}-s\theta_i&-c\theta_i&0&0\c\theta_i&-s\theta_i&0&0\0&0&1&157\0&0&0&1\end{bmatrix}$$

$$_2^1\boldsymbol{T}=\begin{bmatrix}-s\theta_i&-c\theta_i&0&0\0&0&-1&-127\c\theta_i&-s\theta_i&0&0\0&0&0&1\end{bmatrix}$$

$$_3^2\boldsymbol{T}=\begin{bmatrix}c\theta_i&-s\theta_i&0&266\s\theta_i&c\theta_i&0&0\0&0&1&0\0&0&0&1\end{bmatrix}$$

$$_4^3\boldsymbol{T}=\begin{bmatrix}-s\theta_i&-c\theta_i&0&256.5\c\theta_i&-s\theta_i&0&0\0&0&1&-8\0&0&0&1\end{bmatrix}$$

$$_5^4\boldsymbol{T}=\begin{bmatrix}c\theta_i&-s\theta_i&0&0\0&0&-1&-102.5\s\theta_i&c\theta_i&0&0\0&0&0&1\end{bmatrix}$$

$$_6^5\boldsymbol{T}=\begin{bmatrix}-c\theta_i&s\theta_i&0&0\0&0&1&94\s\theta_i&c\theta_i&0&0\0&0&0&1\end{bmatrix}$$

The transformation matrix from the base coordinates to the end-effector is as follows:

$$T={}_1^0T{}_2^1T{}_3^2T{}_4^3T{}_5^4T{}_6^5T$$

The results of the verification using the robot toolbox function in MATLAB are shown in Fig. The established MDH coordinate system and the transformation matrix are consistent with the results of the toolbox transformation matrix calculation.

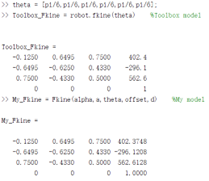
3.MATLAB code